How Unsharp Masking and Laplacian Sharpening WorkThis article offers a full explanation of how unsharp masking and Laplacian (or wavelet) sharpening work. We have all witnessed the magic of unsharp masking and Laplacian sharpening, but many of us do not fully understand what is going on. I believe an indepth understanding will not only alleviate confusion, but will offer insight into how to properly manipulate the controls of an unsharp masking or Laplacian sharpening interface. The first thing to understand is that Laplacian sharpening is simply the application of several unsharp masks simultaneously. As such, an understanding of Laplacian sharpening must first begin with an understanding of unsharp masking. There is no other way to comprehend Laplacian sharpening. The unsharp mask operation actually consists of performing several operations in series on the original image. Those operations, in order, are:
The resulting image (original plus mask) will appear "sharper" to our eye. It is useful to understand why this is the case, as opposed to simply accepting the magic. In short, unsharp masking creates artificial Mach bands. A Mach band is a phenomonen in human vision that all neurology and psychology students learn about. Your eye and your visual cortex perform preprocessing on the retinal image that you "see". There are several forms of preprocessing that occur. An interesting realization is that the world really doesn't "look" like what we see. Our brains twist reality to a remarkable extent before our high centers of reasoning ever get to see what's out there. One form of preprocessing that occurs consists of enhancing edges beyond their true natural appearance. This is call Mach banding. The following graphs show what the eye is doing when is creates Mach bands. 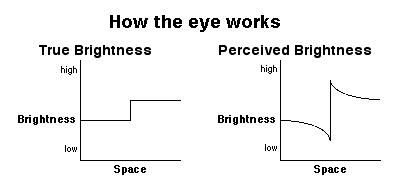
As you can see in the graphs above, when you eye sees an edge corresponding to a brightness change, the eye enhances the edge beyond its true natural appearance, so the visual system can more easily perceive the edge. It does this by pulling the perceived brightness down on the dark side of the edge and up on the light side of the edge. The following image demonstrates Mach bands. The illusion is stunning. 
The reason our brains do this is obvious. By enhancing edges, we can more easily perceive them, which gives us an increased ability to differentiate objects in the world, which is important for all matters of survival. Unsharp masking artificially produces this same phenomenon in an image. Basically it hijacks our Mach banding trick and creates it in the image before you see it. Your brain will perceive the artificial Mach bands the same way it perceives Mach bands that your brain's preprocessing creates, so in short, the edge becomes more starkly apparant to you. So whereever there is a brightness change across some distance of space, unsharp masking makes the darker side of the edge darker and the lighter side of the edge lighter. Since the original image is blurry, it doesn't already have a sharp edge as shown in the graphs above, so the follow graphs are more representative of the effect you get from unsharp masking an image that isn't already sharp. 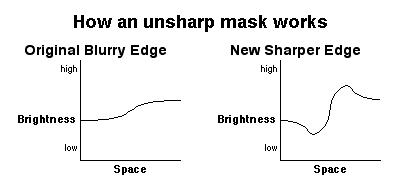
The graphs above show that you don't actually get a vertical edge from unsharp masking, but you do get a steeper brightness change over a given distance of space, which is perceived as a more sudden change in brightness by your eye, or in other words, a sharper edge than in the original. There are two parameters you can control in unsharp masking: the amount of blurring and the scaling factor of the mask. Scaling the mask by a coefficient before adding it to the original increases the degree to which the Mach bands are pulled away from the original brightness curve. The following set of graphs shows that with a small scaling factor you only adjust the original brightness curve by a little bit, but with a large scaling factor you create extremely exagerated Mach bands, which has the perceptive effect of makeing the edge look extremely sharp. Abuse of the scaling factor can lead to unrealistic images because the Mach bands were never really there in the first place, you are creating an artificial edge, so this process must not be used beyond its realistic ability. A given image can only take so much enhancement before you are doing more harm than good. 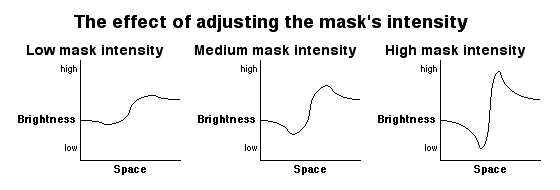
The degree of blurring controls what sized edges the unsharp mask functions on most effectively. Larger stronger blurs produce masks that alter larger edges (the brightness change is spread out over a large distance) but miss smaller edges (where the brightness change happens fairly quickly), while small subtle blurs capture tiny sudden edges but miss larger edges. When using an unsharp mask you must pick a single pair of blur size and mask intensity for the entire image that you think has the most beneficial effect. This is were Laplacian sharpening comes in. Laplacian sharpening blurs an image at several different scales and produces a mask at each level (or layer). The Laplacian transform is a true wavelet transform, which is why this method of sharpening is sometimes generally referred to as a wavelet sharpening, but that's too general since there are countless wavelet transforms, many of which can be used for image enhancement in various ways. Laplacian sharpening is just one of these methods. Laplacian sharpening gives you control over the scaling factor for each of the masks, just the way unsharp masking gave you control over the scaling factor for the single blurred mask that was generated. By strengthening a mask in a "high" layer corresponding to a small blur, you increase the Mach bands in the small features (generally called high frequency components of an image for obvious reasons). By strengthening a mask in a "low" layer corresponding to a large blur, you increase the Mach bands in really large features (which I have noticed has the qualitative effect of enhancing contrast and saturation of an image as much as it sharpens). Middle layers have effects somewhere in the middle. It goes without saying, but the advantage of Laplacian sharpening over unsharp masking is that you can individually control the degree of Mach band generation for edges at different scales in the same image. More control generally means better results. The last thing to realize about Laplacian sharpening is that the interface associated with it has several controls for you to fiddle with. Experimentation and practice are of paramount importance as a result. Good luck! |