September 2001

Capturing a Fourth Dimensional Creature in the Third Dimension

This is an idea I got while reading Edwin A. Abbott's Flatland. Assuming a fourth spatial dimension exists, and assuming beings from that dimension "visit" our dimension by intersecting it (and thus appearing as three-dimensional shapes to us), it is possible to capture certain kinds of shapes and trap them here. In fact, any shape that is not entirely convex should be capturable. I will first show how to capture a two-dimensional creature in one-dimensional space. I will then show how to capture a three-dimensional creature (us) in a two-dimensional space. Finally, I will show how we could capture a fourth-dimensional creature in our three-dimensional space.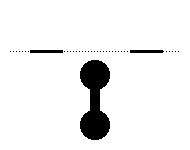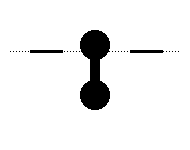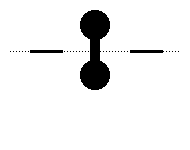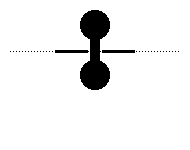

The trick is to allow the being to partially intersect the lower-dimensional space, and then close around its concave structure like a lasso closing around a bull's horns. Notice how this is accomplished when a two-dimensional shape is captured in the first dimension.

Now notice how this logic is extrapolated to capture a three-dimensional shape in the second dimension.

It should be noted at this point that I have not yet illustrated a way in which the captured shape can be viewed. In the second dimension, after the noose closes around the three-dimensional shape intersecting the second dimension, there is no way to see "through" the noose to view the captured shape. This can be modified however, as shown here.

Now, how would this analogy extrapolate to the capture and viewing of a fourth-dimensional shape in the third dimension. It is difficult to draw a picture of this scenario for obvious reasons. But imagine a fourth-dimensional shape that is concave in the fourth dimension. Let's assume the fourth-dimensional equivalant of the barbell shape I have used thus far. As this shape intersects the third dimension it will appear as a sphere that appears from nothing and quickly grows as the bulb of the lower bell passes through the third-dimension. This sphere will then begin to shrink as the second half of the lower bell passes through the third-dimension. At this time, if we wrap the three-dimensional equivilant of a lasso (a hollow sphere for all intents and purposes, basically a beachball) around the sphere, it will be captured. In order to escape (in either direction) the intersecting sphere would have to grow in size first, but it cannot do this because of the enclosing ball. It is even possible to recreate the analogy of a window that allows us to view the captured shape. Simply cut a hole in the ball. We can view through the hole into the interior where the captured intersection of the shape resides (a sphere thrashing around inside the ball trying to escape). The shape still cannot escape so long as the window is not expanded to the size of the ball itself. Nifty, huh?